Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning.
-NCTM, 2014, page 53
When I think about the math teaching practice of eliciting and using evidence of student thinking, I go back to one of the core beliefs that Magma Math was founded on:
How students get the answer is often more interesting than the answer itself.
This teaching practice asks us to take actions that are at the heart of formative assessment:
- Identify what counts as evidence of student progress toward math learning goals
- Elicit and gather evidence of student understanding at strategic points during instruction
- Interpret student thinking to assess mathematical understanding, reasoning, and methods
- Make in-the-moment decisions on how to respond to students with questions and prompts that probe, scaffold, and extend
- Reflect on evidence of student learning to inform the planning of next instructional steps. (Principles to Action, NCTM, 2014, p. 56)
That’s all!! 🙂…. Side note: You may have seen the statistic published a few years ago that teachers make over 1500 educational decisions each day. In an average 6-hour school day that amounts to about one decision every 15 seconds! I’ve heard lots of folks share the imagery that they use to describe the experience of a teacher in the classroom. Whack-a-Mole is one common image. A colleague who is a runner said that teaching is a bit like running in the woods where there are overgrown branches that keep springing up in front of you that you have to navigate. We teachers are making decisions at speed!
Magma Math gives us powerful tools for making instructional decisions at speed!
Magma is a learning environment where students are expected to share their thinking and mathematical processing. This helps teachers look beyond the answers and focus on patterns of reasoning and how these ideas develop over time. When we have access to students’ thinking, we can adjust and differentiate instruction. We can also support our students’ identity development by making their thinking visible. When we display student solutions in Magma and use their ideas to facilitate discussion, we create an environment where our students are resources for each other.
As we teach and monitor student progress, we adjust to best meet the needs of our students. This can be via an entrance or exit ticket where we gather information from our students and use it to plan the next day - perhaps with colleagues. We can also monitor student progress in real-time as they work and make informed decisions in the moment.
For example, I had the opportunity to work with some 6th grade students who were reviewing working with integers. As the students were working on the assignment in the classroom, we posted the heatmap anonymously, and used it to make decisions.
.png)
This heat map reflects student progress at the end of the lesson. As students were working the classroom teacher and I used it to make instructional decisions. Some of the decisions were regarding specific students, and others were about problems.
Focusing on Individual Students
The classroom teacher and I decided to check in with students who had several yellow squares in a row, especially students who had used the check answer feature. We wanted to make sure that they were using that to support their learning in a positive way.
We next looked at student work in the Student Solution view and saw that Student 15 initially had issues with “typos” and used the check solution feature to realize that their answers were correct, but incorrectly written.
When we checked in on what Student 9 was doing, we found a more complex situation. Here are Student 5’s four solution attempts to the problem


We were curious what this student had done for the previous problem that was less complex:
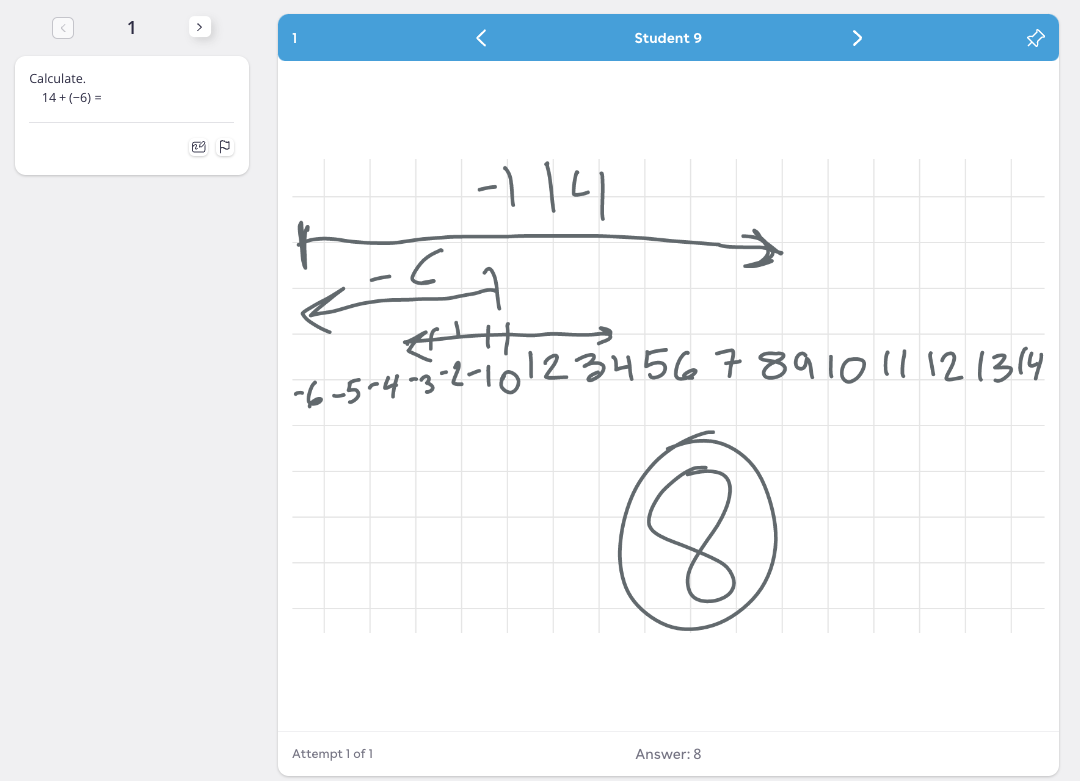
The teacher had a conversation with the student about the method he used for problem #1, and clarified what was going on with the number line (we were a little puzzled), and then the teacher and student worked together to extend the strategy with the number line to solve problem #2 with the larger numbers.
Focusing on a Specific Problem
After a while, we noticed that problem #7 was proving to be problematic for the class as it was turning red on the heat map for most students.
Problem #7: A parking garage goes beneath the ground for several floors. The ground level is 2 meters above mean sea level. Basement 1 is the floor below the ground level and is -3 meters mean sea level. The distance between any two floors is the same. How many meters sea level is Basement 3?
The teacher and I decided to pause the class and have a conversation about the problem, and we realized that the students didn’t have much experience with parking garages or thinking about how they are structured. We read through the problem together and discussed parking garages they had been in. We also realized that these 6th grade students didn’t have a sense of how “tall” 2 and 3 meters were (we asked a tall observer to help make sense of that!). Once we had made more sense of the context of the problem, the students revisited the problem and revised their thinking.
The Power of Feedback
In addition to how we monitor and use student thinking as we teach, one key feedback strategy for powerful formative assessment is to give students immediate feedback whenever possible. In fact, in Visible Learning for Mathematics, John Hattie and fellow authors recommend that we should never delay feedback beyond when it would make a difference for students, and that we should provide feedback as often as is practical (p. 204). When we ask students to work on assignments in Magma, the platform provides students with immediate feedback for each problem. Additionally, Magma is continuing to “get smarter” as more students solve problems, which is enabling us to give smarter and more focused feedback to students. This is SO exciting to me as someone who was able to practice getting a mathematics procedure (long division) wrong for DAYS before learning that I had misunderstood or misremembered!
After the Lesson
At the end of the lesson, we took a moment to look at the data that Magma Math generates. By clicking on the Skill matrix tab at the top left of the heatmap, we were able to see how the students are progressing in the three skills identified in this assignment. In this view, we can see the 3 skills on the left, and the student initials (in this case M1, M2, etc) along the top.

And by clicking on the Stats wheel tab, I can see this view of the data. This view is for the whole class. If I wanted to zoom in, I can look at the pie chart for each student to see how they are progressing. This might be especially helpful for a unit review or assessment.
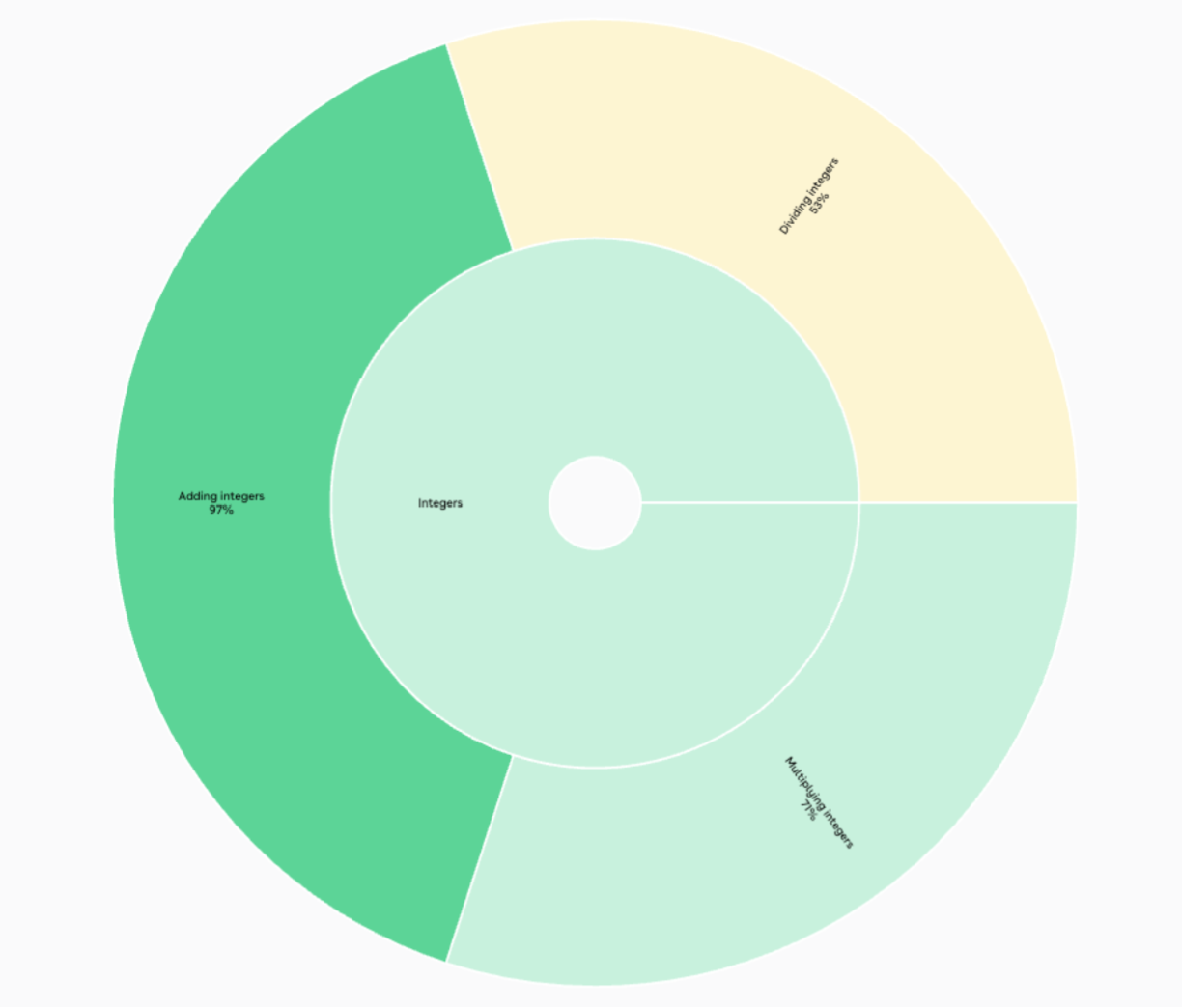
This data helped the teacher determine her next steps in reviewing integers as she moved on to the next topic.
Assessment FOR Learning
The last thing I want to mention in this post is the idea of Assessment for Learning (A4L). A4L comes from the work of Paul Black and Dylan Wiliam and has been elaborated on by Dr. Jo Boaler and the YouCubed team. In an A4L cycle, students need to know three things:
- Where am I now?
- Where do I need to be
- How do I get there
One of the most powerful things we can show students is examples of exemplary or near-exemplary work. As we facilitate discourse with our students, we can share samples of student work. Here is an example of student work for problem #4 that stands out to me.

This is the student’s 5th attempt. What I find delightful is how the student used those attempts to refine their thinking, and then noted in purple that the change is the answer! I would love to share the process of arriving at this solution with the class and discuss how this final solution is strong as well as the process the student followed as an example of how to engage in the mathematical journey. We may dig into this work sample more in the next blog about perseverance!



.jpg)

%20(1).png)


